УДК 517.95

Акимов Андрей Анатольевич,

к.ф.-м.н. наук, доцент,

Стерлитамакский филиал БашГУ, г. Стерлитамак,

Вахитов Алмаз Рустэмович,

студент, Стерлитамакский филиал БашГУ, г. Стерлитамак

Akimov A.A.    

Vahitov A.R.  

ЗАДАЧА ДИРИХЛЕ ДЛЯ ЭЛЛИПТИЧЕСКОГО УРАВНЕНИЯ С СИНГУЛЯРНЫМ КОЭФФИЦИЕНТОМ

The Dirichlet problem for an elliptic equation with a singular coeficient

 Аннотация

В работе рассмотрена задача Дирихле для эллиптического уравнения с сингулярным коэффициентом. При определенных ограничениях на границу области и коэффициенты уравнения доказаны единственность решения в классе функций, след которых представимых в виде суммы ряда Фурье и существование решения поставленной задачи.

S u m m a r y

In this paper we consider the Dirichlet problem for an elliptic equation with a singular coefficient. Under certain restrictions on the boundary of the domain and the coefficients of the equation, the uniqueness of the solution in the class of functions whose trace is representable as the sum of a Fourier series and the existence of a solution of the posed problem are proved.

Ключевые слова: эллиптическое уравнение, задача Дирихле, сингулярные уравнения, краевые задачи, Фурье

Keywords: elliptic equation, Dirichlet problem, singular equations, boundary value problems, Fourier

1. Постановка задачи.

   Рассмотрим уравнение эллиптического типа

где  в области эллиптичности D – единичном квадрате со сторонами 

   Для уравнения (1) при  в области D поставим краевую задачу:

   Найти в квадрате D функцию  удовлетворяющую условиям:

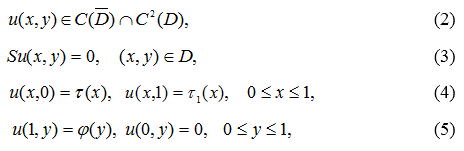
где  заданные, достаточно гладкие функции, 

   В  работе [1] были доказаны единственность и существование решения задачи, аналогичной (2) – (5) при  в произвольной области, лежащей в полуплоскости  и ограниченной линией  Была построена теория потенциала уравнения (1) при и получена формула решения через функцию Грина. Для полукруга построена функция Грина и в явном виде выписано решение задачи.

   В работе [2] для уравнения (1) при  в четверти круга  построено решение краевой задачи с нелокальным условием на линии  в виде суммы биортогонального ряда. Решение этой задачи использовалось при построении решения задачи Трикоми.

   Для уравнения (1) Сабитовым К.Б. доказан принцип максимума, который можно использовать для доказательства единственности решения задачи.

   В данной работе используется спектральный метод [4] для решения задачи (2) – (5) при 

2. Построение частных решений методом разделения переменных.

   Пусть функция  является решением задачи (2) – (5). В уравнении (1) разделим переменные, представив

и подставив (6) в (1):

   Разделим обе части последнего равенства на произведение 

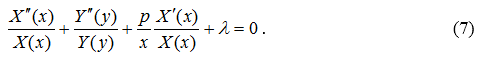
   Уравнение (6) перепишем в виде

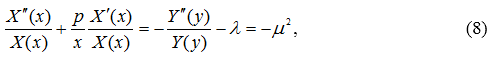
где 

– некоторая константа.

   Левая часть равенства (8) зависит только от x,  а правая часть только от y, поэтому равенство (8) возможно только тогда, когда правая и левая части представляют одну и ту же постоянную  —  Тогда из соотношения (8) получим два обыкновенных дифференциальных уравнения второго порядка:

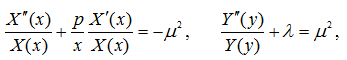
или равносильные им уравнения

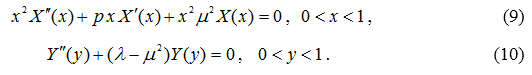
   Найдём общее решение уравнения (9). Заменяя функцию  получим уравнение Бесселя

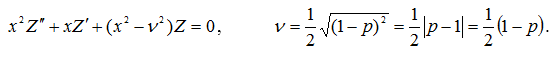
   Записывая общее решение уравнения Бесселя в виде

где  – функция Бесселя первого рода,  – функция Бесселя второго рода,  – постоянные, получим общее решение уравнения (8) в виде

   Так как  при  обращается в бесконечность, то ограниченным решением уравнения (8) будет (10) при то есть

   Найдём общее решение уравнения (10). Составим характеристическое уравнение, соответствующее уравнению (10):

   Тогда общее решение уравнения (10) имеет вид:

1) при 

с некоторыми постоянными 

2) при 

с некоторыми постоянными 

   Итак, ограниченное в области D  решение уравнения (1) есть функция

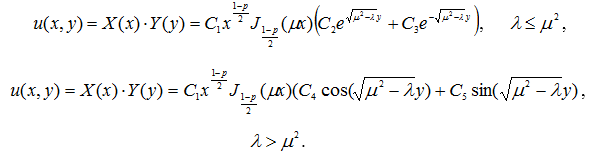
   Пусть решение задачи (2) – (5) при  то есть, выполнены равенства

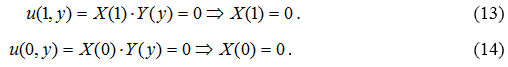
   Следовательно, функция  из формулы (6) является решением следующей спектральной задачи: найти значения параметра  и соответствующие им функции  которые удовлетворяют уравнению (9) и граничным условиям (13) и (14).

   Для решения этой спектральной задачи воспользуемся ограниченным при   решением (12) уравнения (9), которое удовлетворим условиям (13) и (14):

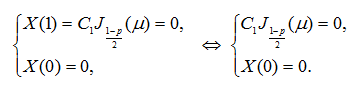
   Исходя из первого уравнения системы имеем  так как, в противном случае, получим тривиальное решение,  Так как нули функции Бесселя при  положительны и счетны, то обозначим через  – n-ый положительный корень функции 

   Итак, система функций

где  – положительный вещественный корень бесселевой функции  является системой собственных функций спектральной задачи (9), (13), (14), соответствующей множеству собственных значений 

   Вернёмся к уравнению (7). Его можно переписать в виде

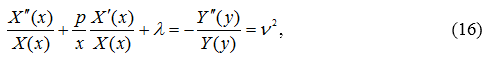
или

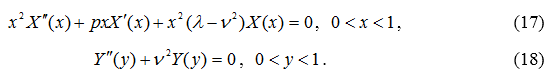
   Общее решение уравнения (17) имеет вид [7, с.401]:

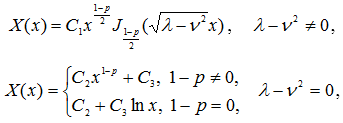
где  – некоторые постоянные.

   Общее решение уравнения (18) есть функция

с постоянными 

   Тогда ограниченное в области D  решение уравнения (1) можно представить в виде

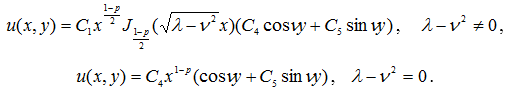
   Предположим, что  решение задачи (2) – (5) при  Тогда можно показать, как это проделано для функции  , что параметр  и соответствующая функция  являются решением спектральной задачи для уравнения (18) со следующими условиями

   Используя функцию (19), получим,

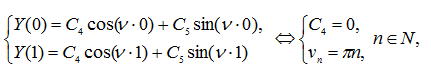
т.е. решением спектральной задачи (18), (20) являются собственные значения  и соответствующие им собственные функции

3. Единственность решения.

Теорема 1. Если существует решение задачи (2) – (5) при  то оно единственно.

Доказательство.

   Рассмотрим функции

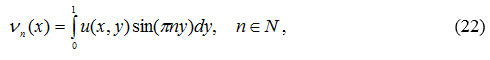
которые при фиксированном y есть коэффициенты разложения Фурье функции  в ряд по  Покажем, что  удовлетворяет обыкновенному дифференциальному уравнению:

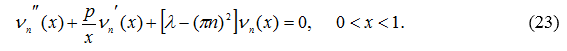
   Действительно

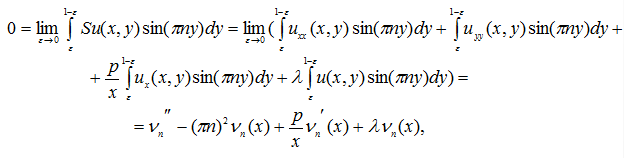
так как

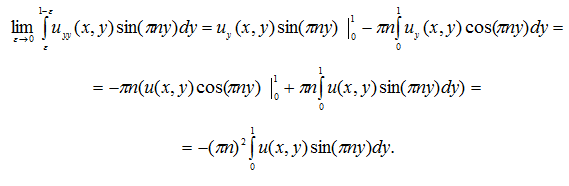
   Положив в формуле (22)  получим, что

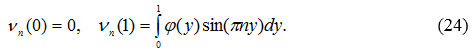
1) При  общее решение уравнения (23) имеет вид [7, с.401]

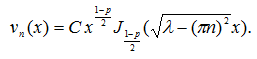
   Удовлетворяя общее решение условиям (24) получим

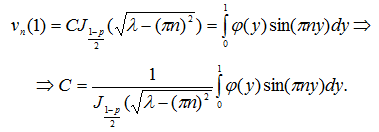
   Таким образом, решение задачи (23), (24) есть функция

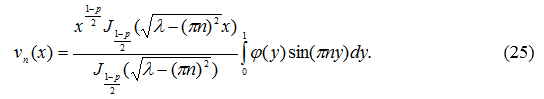
2) При  общее решение уравнения (23) имеет вид [7, с.401]

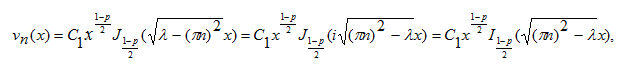
   Из условий (24) найдем константу 

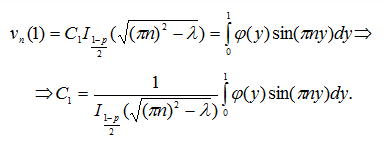
   Таким образом, решение задачи (23), (24) есть функция

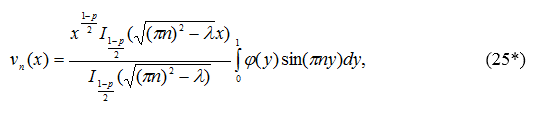
где  – модифицированная функция Бесселя порядка 

3) При  общее решение уравнения (23) имеет вид [7, с.401]

где  неизвестные пока постоянные.

   Так как  то получим что  то получим что 

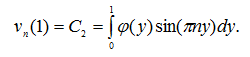
   Таким образом,  решение задачи (23), (24) есть функция

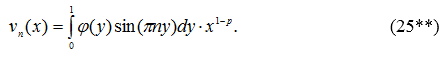
   Из формул (25), (25*), (25**) и теории рядов Фурье следует единственность решения задачи (2) – (5), так как, если  на сегменте [0,1], при этом  интегрируема (так как  непрерывна на  ), все коэффициенты ряда Фурье функции 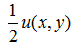 равны нулю, так как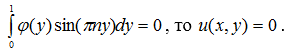  

4. Существование решения.

Теорема 2. Если то существует единственное решение задачи (2) – (5) при    и оно имеет вид

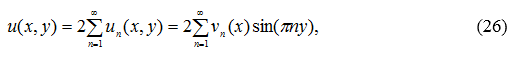
где  

определяется формулами  (25), (25*), (25**) .

Доказательство.  В теореме 1 пункта 3 показано, что если существует решение  задачи (2) – (5), то оно имеет вид (26). Остается обосновать, что функция  принадлежит классу (2), удовлетворяет уравнению (3) и краевым условиям (4), (5).

   Покажем, что функция  Обоснуем что  Для этого покажем, что ряд в формуле (26) равномерно сходиться в  

   Оценим члены функционального ряда в (26).

   Пусть  тогда  определяется по формуле (25). Так как функция 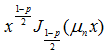 ограничена на бесконечности, имеем оценку:

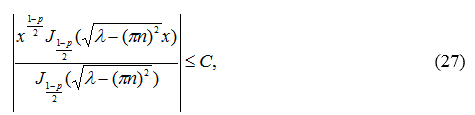
где C — некоторая константа.

   Оценим интеграл

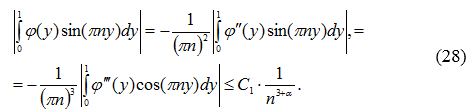
   Эта оценка следует из работы [6, с.81].

   Из оценок (27), (28) следует, что

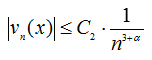
и ряд в (26)  мажорируется положительным числовым рядом 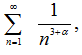 значит по признаку Вейерштрасса сумма ряда (26) непрерывна в .

2) Пусть    тогда   определяется по формуле (25*). Имеет место оценка:

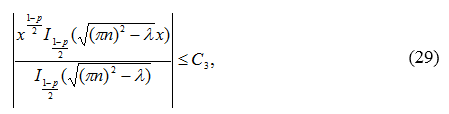
где  — некоторая константа.  Из оценок (28), (29) имеем

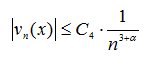
и ряд в (26) мажорируется 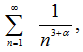 значит по признаку Вейерштрасса сумма ряда (26) непрерывна в .

3) При   определяется по формуле (25**).

   Оценим интеграл

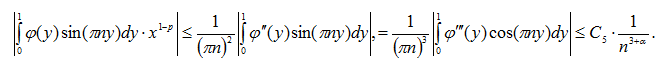
   Тогда 

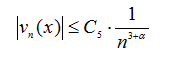
и ряд мажорируется 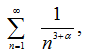 значит по признаку Вейерштрасса сумма ряда (26) непрерывна в .

   Покажем, что   Для этого продифференцируем ряд по x и y два раза в области D.

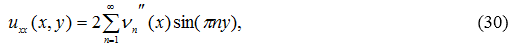
1) при  

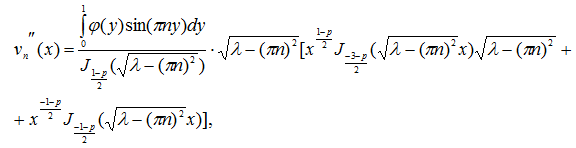
б) при 

   Оценим функциональный ряд (30). Имеем

   В силу ограниченности на бесконечности функции  имеем оценки:

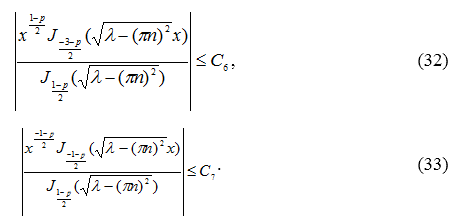
   Из оценок (28), (31), (32), (33), следует, что 

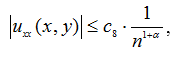
то есть ряд в формуле (30) мажорируется сходящимся положительным числовым рядом, следовательно, равномерно сходиться на D.

   Продифференцируем ряд по y два раза в области  D

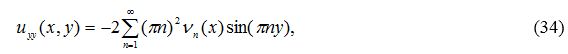
   При любом  справедлива оценка

   Из этой оценки следует, что 

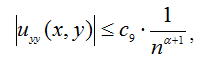
то есть ряд в формуле (35) мажорируется сходящимся положительным числовым рядом, следовательно, равномерно сходиться на D.

   Покажем, что функция (26) удовлетворяет краевым условиям (4), (5). Для этого докажем сходимость к функциям  их разложений.

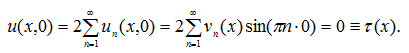
   Аналогично, 

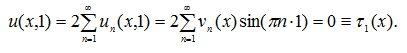
   Удовлетворим  условию (5):

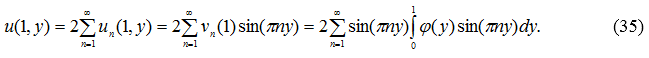
   Так  как   имеет ограниченное изменение на [0,1], то по признаку Дирихле Жордана [6, c.98] ряд (29) сходится к .

Список литературы

1. Пулькин, С.П. Некоторые краевые задачи для уравнения 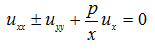/ С.П. Пулькин // Уч. зап. Куйбыш. пединститута., 1958, Вып. 21.
2. Сабитов, К.Б., Ильясов, Р.Р. Решение задачи Трикоми для уравнения с сингулярным коэффициентом спектральным методом / К.Б. Сабитов, Р.Р. Ильясов // Изв. вузов. Матем. – 2004. – № 2.
3. Ильясов, Р.Р. Задачи Коши и Гурса для гиперболического уравнения с сингулярным коэффициентом / Р.Р. Ильясов // Труды Всеросс. науч. конф. “Современные проблемы физики и математики.” – Уфа: Гилем, 2004.
4. Моисеев, Е.И. О решении спектральным методом одной нелокальной краевой задачи / Е.И. Моисеев // Дифференц. уравнения. – 1999. – Т. 35, № 8.
5. Ватсон, Г.Н. Теория бесселевых функций / Г.Н. Ватсон. – Ч.1.– М: ИЛ, 1949.
6. Зигмунд, А. Тригонометрические ряды. / А. Зигмунд. – М: Мир, 1965.
7. Камке, Э. Справочник по обыкновенным дифференциальным уравнениям [Текст] / Э. Камке. – М: ИЛ, 1949.  
8. Сабитов К.Б., Акимов А.А. К теории аналога задачи Неймана для уравнений смешанного типа // Известия высших учебных заведений. Математика. 2001. № 10. С. 73 — 80.
9. Акимов А.А. О единственности решения задачи типа Неймана для уравнения Чаплыгина // Вестник Московского государственного областного университета. 2013. № 4. С. 38.
10. Акимов А.А., Агафонова А.А. Из истории построения функции Римана-Грина // Современные научные исследования и разработки. 2017. № 7 (15). С. 35-38.
11. Акимов А.А., Абдуллина Р.И. Использование функциональных рядов при решении интегральных уравнений // Синергия Наук. 2017. № 14. С. 871-876.
12. Акимов А.А., Абдуллина Р.И. Методика построения функции Римана-Грина // Colloquium-journal. 2017. № 10 (10). С. 76-79.