УДК 517.95

Акимов Андрей Анатольевич,

к.ф.-м.н. наук, доцент,

Стерлитамакский филиал БашГУ, г. Стерлитамак,

Вахитов Алмаз Рустэмович,

студент, Стерлитамакский филиал БашГУ, г. Стерлитамак

Akimov A.A.    

Vahitov A.R.  

УРАВНЕНИЕ ЛАВРЕНТЬЕВА-БИЦАДЗЕ С КРАТНЫМИ ХАРАКТЕРИСТИКАМИ

LAVRENTIEV-BITSADZE EQUATION WITH MULTIPLE CHARACTERISTICS

Аннотация

В данной работе исследуются две краевые задачи для модельного уравнения Лаврентьева-Бицадзе с одним семейством характеристик, дважды пересекающих линию изменения типа. Краевые задачи для таких уравнений сводятся к эллиптическим краевым задачам со смещениями и сингулярным интегральным уравнениям со смещением. Получена  распадающаяся система сингулярных уравнений в случае, если граница эллиптической части берётся нормальной кривой и не распадающаяся система полных сингулярных уравнений в случае произвольной границы класса Ляпунова.

S u m m a r y

In this paper we study two boundary value problems for the Lavrent’ev-Bitsadze model equation with one family of characteristics that twice cross the line of change of type. Boundary value problems for such equations reduce to elliptic boundary-value problems with displacements and singular integral equations with displacement. A disintegrating system of singular equations is obtained in the case when the boundary of the elliptic part is taken by a normal curve and the decomposable system of complete singular equations in the case of an arbitrary boundary of the Lyapunov class.

Ключевые слова:  модельное уравнение Лаврентьева-Бицадзе, сингулярные уравнения, краевые задачи, класс Ляпунова

Keywords:  Lavrent’ev-Bitsadze model equation,  singular equations,  boundary value problems, Lyapunov class

1. Постановка задачи. Рассмотрим уравнение

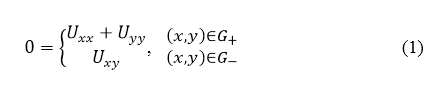
на множестве где  — область, ограниченная прямыми x – y = 0 и x + y = 0 и кривой Г из класса Ляпунова,  — область, ограниченная прямыми x – y = 0, x + y = 0, y =  –d.

   Обозначим  где 

Задача 1. Найти функцию   удовлетворяющую следующим условиям:

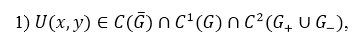
т.е. вдоль ломаной АОВ – непрерывная склейка по функциям  и  (эти производные могут обращаться в  в точках А, О, В).

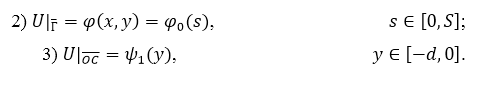
где  — заданные достаточно гладкие функции.

Задача 2. Отличается от задачи 1 тем, что условие 3) заменяется на

   Производные  в точках А и В могут обращаться в  порядков меньше 1.

2. Соотношения на линии изменения типа. Теоремы единственности.

   Применим отображение

где   конформное везде, кроме точки О.

   Область   преобразуется в область  системы координат ограниченную снизу отрезком  оси  

   Выведем соотношение между частными производными на  и  

   Для этого сначала найдем формулы преобразования в декартовых координатах.

   Возведем (2) в квадрат:

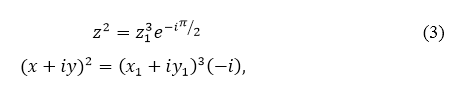
так как 

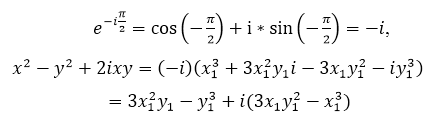
   Отсюда имеем

   Из формулы (3) следует

   Тогда

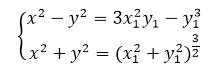
или

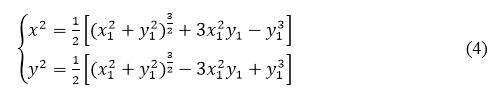
   Соотношения (4) и есть искомые формулы преобразования.

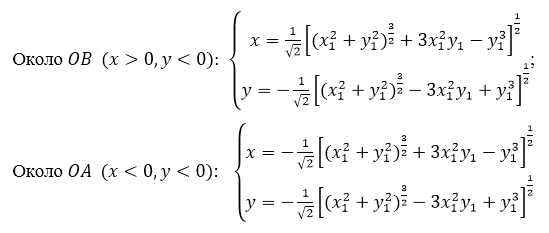
   В силу соотношений (4) координаты   на  будут следующими:

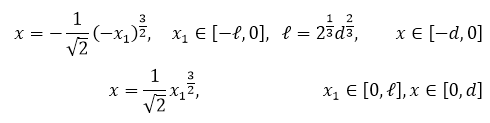
   Формулы связи между производными на АО:

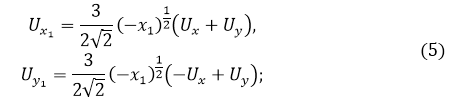
на ОВ:

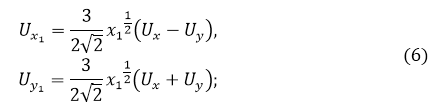
   Из соотношений (5) получим на АО:

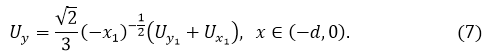
   А из соотношений (6) получим на ОВ: 

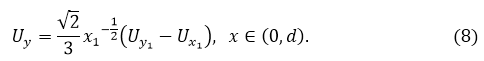
   Так как в  вдоль прямых   то обозначив  имеем на 

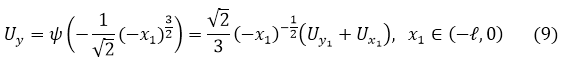
   На 

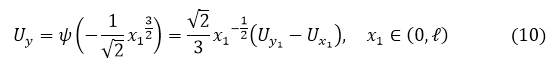
   Перейдем к переменным

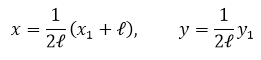
   В области  вид уравнения (1) не изменится:

   Обозначим  на  на   на  на 

   Соотношения (9), (10) примут вид:

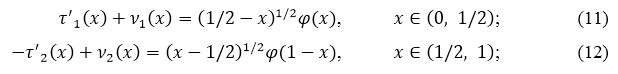
где   

   Докажем единственность решения задачи. В случае однородной задачи 1  для функции   имеем

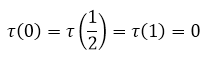
   Значит,  достигает максимума или минимума в некоторой точке    из (0, 1/2) или (1/2, 1). Тогда 

   Из соотношения (11) или (12) следует  что противоречит принципу Зарембо-Жиро, в силу которого  Отсюда следует что 

  В случае однородной задачи 2  на прямых  т.е.  отсюда 

3. Сведение задачи 1 к системе сингулярных уравнений.  Задачу будем решать в случае, когда кривая Г и ее образ  — дуги окружностей с центром в начале координат и в точке (1/2, 0).

   На линии  имеет место соотношение между функциями  из эллиптической части [4]

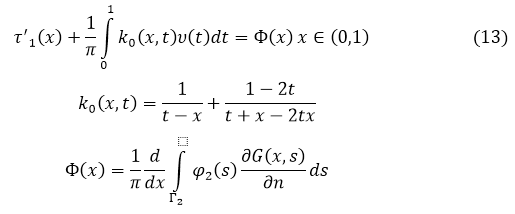
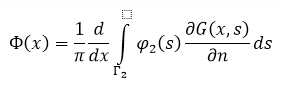
где  — образ функции 

   Наложим условия 

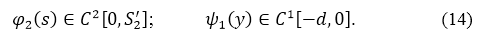
   Тогда

   Напишем соотношение (13) для 

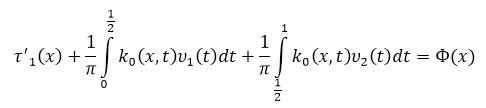
   Во втором интеграле заменим t на 1 — t и с учетом  получим:

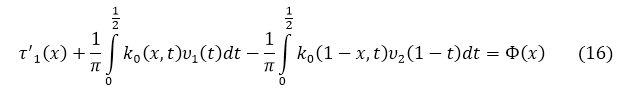
   Аналогично при 

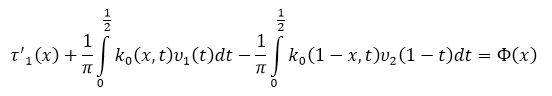
   Заменим x на (1 — x), тогда:

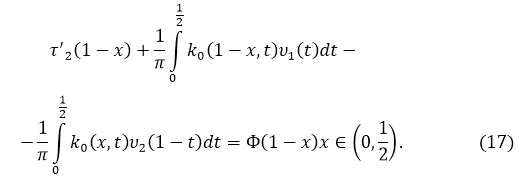
   Сложим и вычтем соотношения (16) и (17):

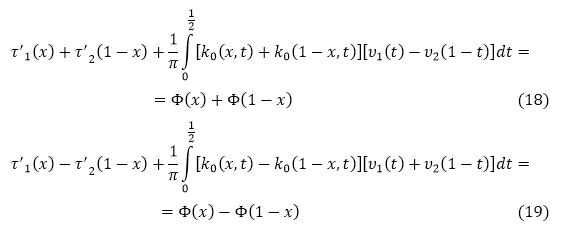
   Из (11) и (12) следует

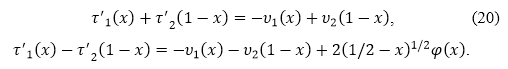
   Подставив полученное в (18), (19), обозначив               

получаем систему сингулярных уравнений

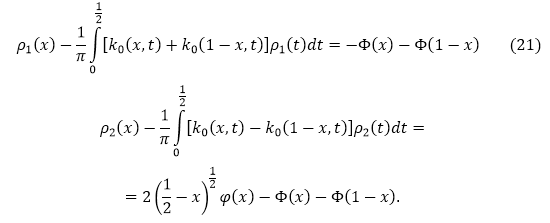
   Перейдем к переменным

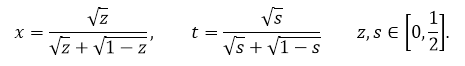
   Тогда

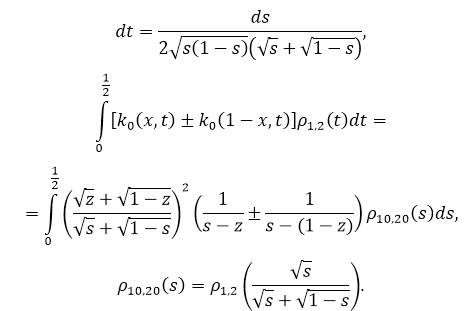
   Уравнения (21), (22) примут вид

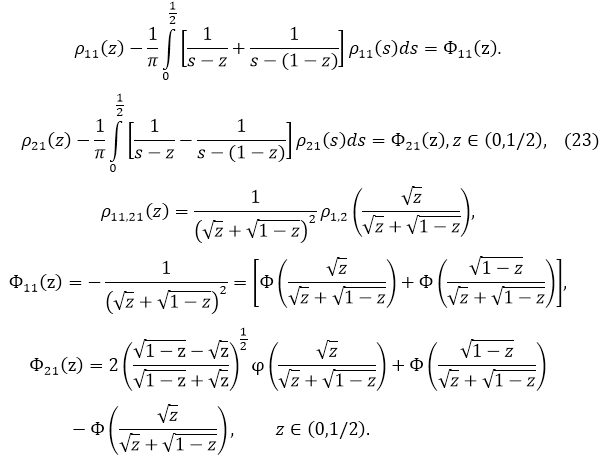
   Функции  непрерывны на [0, 1/2] и удовлетворяют на нем условию Гёльдера с показателем 1/2 (так как их производные при  в бесконечность порядка 1/2). 

   Перейдём в уравнениях (23) к переменным  по формулам

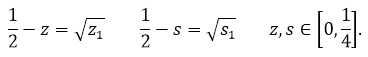
   Интегралы в них принимают вид

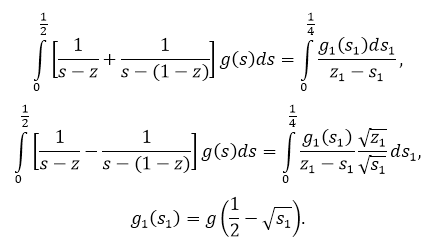
   Уравнения (23) принимают вид

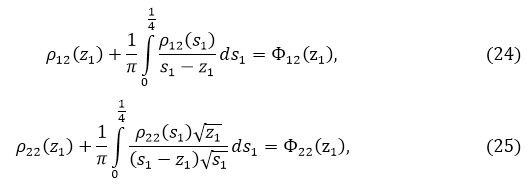
где

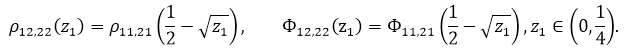
   Функции  непрерывны на [, 1/4] и удовлетворяют условию Гельдера с показателем 1/4 (то есть принадлежат классу Мусхелишвили). Это требуется для разрешимости сингулярных уравнений.

4. Решение сингулярных уравнений. Решаем сингулярные уравнения (24) , (25) по алгоритму из монографии [5]. Согласно классу решений задач 1 и 2 их решения следует искать в классе функций, ограниченных в точке  и допускающих обращение в бесконечность порядка меньше 1 при 

   Найдем из 

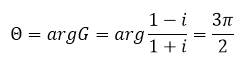
   Индекс уравнений (24), (25)

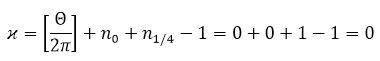
то есть, в рассматриваемом классе решений они однозначно разрешимы.

   Найдем показатели степеней

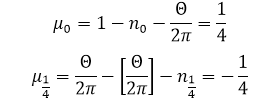
   Решения уравнений (24), (25)

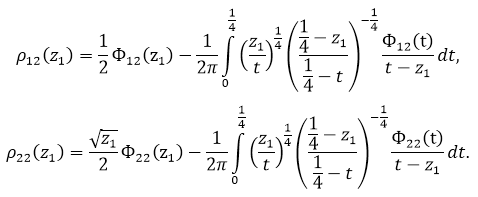
   Эти решения при  могут обращаться в  порядка 1/4. Зная теперь  находим  затем из системы (20’) находим

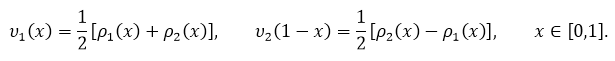
   Затем из (20) находим  Зная эти функции, находим известными методами решение задачи 1 в областях 

Решение задачи 2. Обозначив    из соотношений (5) и (6) находим на АО:

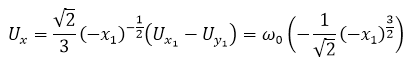
на ОВ:

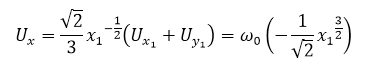
   Аналогично соотношениям (11), (12) в переменных

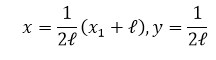
получим

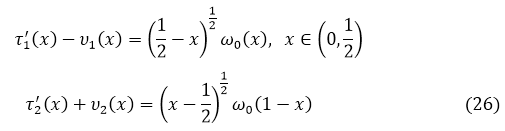
   Далее совершенно аналогично тому, как в пункте 3, приходим к системе сингулярных уравнений

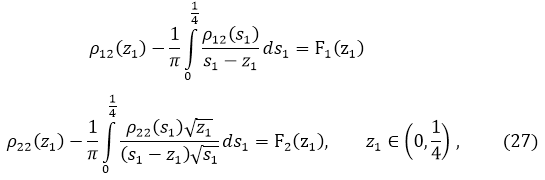
где  — те же, что и в § 3;

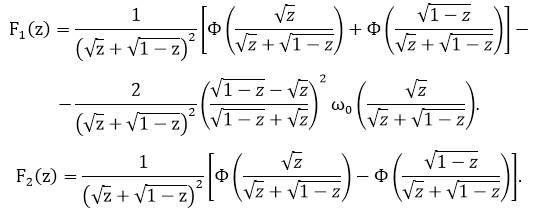
 (Класс Мусхелишвили).

   Уравнения (27) решаем в том же классе решений, что и в задаче 1 (их индекс в этом классе равен 0)

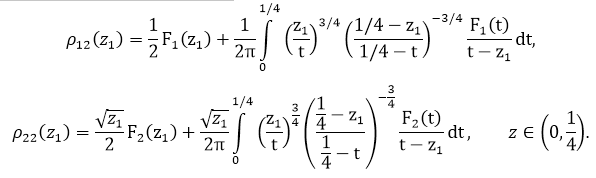
   Эти решения ограничены в точке  и обращаются при  в бесконечность порядка 1/4.

Литература

1. Кузьмин А.Г. Неклассические уравнения смешанного типа и их приложения к газодинамике. Изд-во Ленинградского гос. Университета, 1990 г. 208 стр.
2. Моисеев Е.И. Дифференциальные уравнения. 1992 г. т.28 № 7, С. 1128-1137
3. Сабитов К.Б., Исянгильдин А.Х. Задача типа Трикоми с нелокальными условиями сопряжения для однородного уравнения смешанного типа. ДАН. 1992 г. т.326 № 5 с.787-791
4. Бицадзе А.В. Некоторые классы уравнений в частных производных. М.: Наука, 1981 г. с. 488
5. Самко С.Г., Килбас А.А., Маричев О.И. Интегралы и производные дробного порядка и некоторые их приложения. — Минск: Наука и техника, 1987г. с.688
6. Сабитов К.Б., Акимов А.А. К теории аналога задачи Неймана для уравнений смешанного типа // Известия высших учебных заведений. Математика. 2001. № 10. С. 73 — 80.
7. Акимов А.А. О единственности решения задачи типа Неймана для уравнения Чаплыгина // Вестник Московского государственного областного университета. 2013. № 4. С. 38.
8. Акимов А.А., Агафонова А.А. Из истории построения функции Римана-Грина // Современные научные исследования и разработки. 2017. № 7 (15). С. 35-38.
9. Акимов А.А., Абдуллина Р.И. Использование функциональных рядов при решении интегральных уравнений // Синергия Наук. 2017. № 14. С. 871-876.
10. Акимов А.А., Абдуллина Р.И. Методика построения функции Римана-Грина // Colloquium-journal. 2017. № 10 (10). С. 76-79.