УДК 519.852

ДВОЙСТВЕННОСТЬ В ЗАДАЧЕ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ОГРАНИЧЕНИЯМИ КОНУСНОГО ТИПА

DUALITY IN THE TASK OF LINEAR PROGRAMMING WITH CONE TYPE RESTRICTIONS

Старкова Екатерина Олеговна, Пермский национальный исследовательский политехнический университет

Научный руководитель: Севодин Михаил Алексеевич, кандидат физико-математических наук, доцент, Пермский национальный исследовательский политехнический университет

Starkova E.O.

Scientific adviser: Sevodin M.A.

Аннотация: Статья посвящена исследованию связи задачи линейного программирования с ограничениями конусного типа и паре двойственных к ней задач. Рассмотрен перенос исходной прямой задачи в пространство новых переменных, вследствие чего появляется новая задача, к которой также строится двойственная. Доказаны теоремы и свойства двойственности для таких задач, а также их экономическая интерпретация. Показано, что некоторые экономические характеристики производственного процесса не меняются при переходе в новое пространство. Выявленные свойства могут быть полезны как для анализа предприятия, так и для решения многих экономических задач.

Summary: The article is devoted to the study of the relationship of a linear programming problem with cone-type constraints and a pair of dual problems to it. It is proposed to transfer the original problem into the space of new variables, as a result of which a new problem appears, to which a dual one is also being constructed. Theorems and properties of duality for such problems, as well as their economic meaning, are considered. It is shown that some production indicators, for example, the marginal rate of substitution or marginal utility, do not change when moving to a new space. The revealed properties can be useful both for the analysis of the enterprise, and for solving many economic problems.

Ключевые слова: ограничения конусного типа, линейное программирование, двойственность.

Keywords: cone constraints, linear programming, duality.

Введение. Бурное развитие экономической теории и математической экономики в частности во многом стимулируется как запросами производства, так и непосредственным развитием самих этих наук. В полной мере это относится и к теории линейного программирования. В результате таких процессов исследований, например, была создана теория двойственности, которая может быть успешно применена для решения широкого спектра экономических задач, и без которой нельзя представить современную теорию линейного программирования.

Понятие двойственности является одним из важнейших в линейном программировании. В основе данной теории лежит постулат: для любой задачи линейного программирования можно составить некоторую другую задачу линейного программирования, решение которой тесно связано с решением исходной. Такая задача называется двойственной к исходной (прямой) задаче. [1].

Теория двойственности оказалась полезной для проведения качественных исследований задач линейного программирования. В ходе исследования взаимосвязи прямой и двойственной задач были обнаружены их определенные свойства, позволяющие проводить глубокий экономический анализ предприятия прямо в процессе планирования деятельности и на основе результатов предоставленного анализа давать рекомендации предпринимателям для принятия обоснованных решений.

В статье рассматривается задача линейного программирования с конусными ограничениями и двойственная к ней задача. Предлагается перенести исходную задачу в новое пространство. Базисом такого пространства будет являться набор векторов, который представляет собой систему образующих конус векторов [2]. В результате образуется новая задача уже с меньшим количеством ограничений, для которой строится другая двойственная задача. После чего рассматриваются экономический смысл построенных задач и их свойства двойственности. В заключении доказывается, что такие характеристики, как предельная полезность и предельная норма замещения, инвариантны при переносе производственной задачи линейного программирования с конусными ограничениями в пространство новых переменных.

Постановка задачи. Рассмотрим прямую задачу линейного программирования с конусными ограничениями:

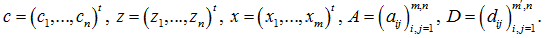
где

Здесь «t» — знак транспонирования.

Условие на вектор z называется ограничением конусного типа, если выполняется свойство: если для любого   

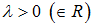
вектор z удовлетворяет определенному условию, то  

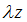
удовлетворяет этому условию [2].

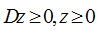
По конусным ограничениям

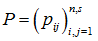
строится матрица перехода

из Rⁿ в многогранный выпуклый конус T и формируется новая задача в новом базисе, но уже с меньшим количеством ограничений [2]. Здесь матрица перехода имеет размер n_xs, где n – число переменных задачи (1), а s – число образующих многогранного выпуклого конуса.

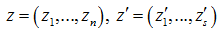
Пусть

— вектор переменных в старом и новом базисах соответственно. Тогда старые координаты будут выражаться через новые по формуле: z=Pz^’. На основании этих утверждений в новом базисе, который состоит из набора векторов, являющегося системой образующих конус векторов, формируется следующая задача:

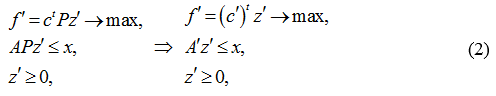
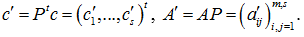
где

Следует подчеркнуть, что в силу перевода задачи (1) в другое пространство количество ограничений у задачи (2) становится меньше, чем у ее оригинала (1).

Составим двойственную задачу к задаче (1):

и двойственную задачу к задаче (2):

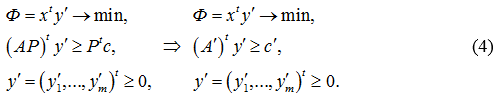
В дальнейшем задачу (4) будем называть T-двойственной к прямой задаче (1).

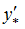
Оптимальный T-двойственный план

задачи (4) в общем случае можно построить по оптимальному базисному плану z_* задачи (1), который можно найти по известным схемам. Например, с помощью симплекс-метода. В этом случае, используя последнюю симплекс-таблицу, можно определить следующее:

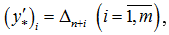
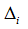
— это оценки столбцов последней симплекс-таблицы, т.е. это оценки оптимального базисного плана.

Известный критерий оптимальности решения при отыскании максимума линейной функции симплексным методом заключается в проверке оценок столбцов симплекс-таблицы (по-другому, симплексных разностей) на неотрицательность.Критерий оптимальности. Для решения задачи (1) симплекс-методом требуется привести задачу к каноническому виду. Количество переменных задачи (1) увеличится на m+m^’, и ее опорный план z_* будет оптимален тогда и только тогда, когда все разности

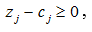
где

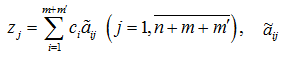
— это элемент симплексной таблицы, стоящий на пересечении i-ой строки и j-го столбца.

Обсудим некоторые свойства решений задач (1) – (4). Экономический смысл двойственных задач. Рассмотрим некоторое предприятие, выпускающее n типов продукции и использующее при этом m видов производственных факторов (ресурсов). Обозначим через a_ij – количество i-го ресурса, которое необходимо для производства единицы j-ой продукции; z_j – количество единиц выпускаемой продукции j-го типа; x_i – запас i-го ресурса; c_j — цена единицы продукции j-го типа. Задача (1) сводится к следующему: найти такой вектор переменных z=(z₁,…,z_n)^t, при котором стоимость всей продукции c^tz была максимальной, и который бы удовлетворял ограничениям на ресурсы

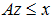
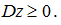
и конусным ограничениям

Если продолжать рассматривать задачу (1) как производственную задачу максимизации стоимости всей продукции, то тогда в результате ее перевода в новое пространство задача (1) модифицируется и появляется новая задача (2), описывающая совершенно другое предприятие. Назовем это предприятие фиктивным. У данного фиктивного предприятия тот же уровень ресурсов x, но уже другие цены на выпускаемую продукцию c^’ и нормы расхода ресурсов A^’. Цель производства такого предприятия остается прежней – максимизация дохода, однако план выпуска продукции z^’ будет отличаться от плана z, и эти планы будут связаны неравенством z=Pz^’.

На основе тех же данных может быть поставлена другая задача (4) – фиктивная двойственная задача к задаче (2), которая одновременно является и T-двойственной задачей к задаче (1). В ней переменными являются оценки, соответствующие каждому виду ресурсов. Обозначим через

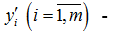
цены на единицу x_i-го ресурса. Эти переменные назовем T-двойственными теневыми оценками (ценами) ресурсов, которые должны удовлетворять ограничению

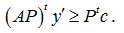
Данное неравенство показывает, что общая оценка (стоимость) затрачиваемых ресурсов не должна быть меньше стоимости окончательного продукта. Общая стоимость всех имеющихся ресурсов равна x^ty^’. В отличие от «внешних» (известных) цен на выпускаемую продукцию, цены ресурсов являются «внутренними» [3], т.к. это есть оценка ресурсов только в рамках рассматриваемой задач. Таким образом, получается следующая экономическая задача (4): с учетом заданного объема ресурсов x требуется найти такие «внутренние» теневые цены y^’ на эти ресурсы при заданных «внешних» ценах P^tc и известных оценках норм расхода ресурсов AP, чтобы общая стоимость затрат была наименьшей.

Свойства решений Т-двойственной задачи. T-двойственная задача обладает многими свойствами двойственной задачи, в частности каждому неконусному неравенству в пространстве прямой задачи (1) соответствует переменная в пространстве T-двойственной задачи (4). Рассмотрим ряд теорем и следствий. Обозначим через z_*, y_*, y_/^’ — оптимальные решения прямой, двойственной и Т-двойственной задач соответственно.Первая теорема двойственности. Если одна из задач (1) и (4) разрешима, то и вторая разрешима, причем f(z_*)=Ф(y_*^’).

Данная теорема говорит о том, что в случае оптимального решения предприятие находится в точке рыночного равновесия. Другими словами, предприятию безразлично, производить ли дальше продукцию в количестве z_* с использованием ресурсов в количестве x, или же продать (сдать в аренду) это же количество ресурсов x по ценам y_*^’, так как в обоих случаях предприятие получит один и тот же доход [4].

Следствие: выполняется равенство y_*=y_*^’, причем F(y_*)=Ф(y_*^’). Это следствие показывает, что найдя оптимальное решение двойственной задачи (3), мы найдем решение Т-двойственной задачи. Обратное неверно, т.к. помимо вектора y задача (3) имеет вектор переменных

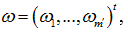
отвечающий за конусные ограничения в прямой задаче (1).

Вторая теорема двойственности. Для прямой задачи (1) и Т-двойственной к ней (4) на оптимальных векторах z_* и y_*^’ выполняются равенства

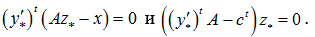
Данная теорема есть необходимое условие оптимальности решений z_* и y_*^’. Для того, чтобы условие было и достаточным, требуется, чтобы найденное решение прямой задачи (1) z_* принадлежало построенному конусу, т.е. удовлетворяла конусным ограничениям:

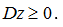
Эта теорема показывает, что Т-двойственная оценка (y_*^’) есть мера дефицитности i-го ресурса. Если (y_*^’)_i=0, то тогда ресурс x_i — избыточный (используется не полностью), иначе при (y_*^’)_i>0 ресурс x_i — дефицитный. Очевидно, чем больше значение оптимальной теневой оценки, тем выше дефицитность ресурса [5].

Третья теорема двойственности описывается равенством:

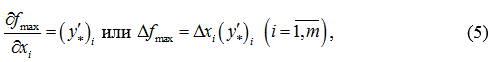
которое представляет теневые Т-двойственные оценки в качестве меры влияния на значение целевой функции. Величина оценки некоторого ресурса показывает, насколько увеличится максимальное значение целевой функции

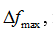
при увеличении запаса данного ресурса на единицу [6].

Функция полезности. Вернемся обратно к постановке прямой задачи производственного потребления (1), в которой требовалось найти план производства z для доступной совокупности ресурсов x. Полезность набора x можно оценить по-разному, в зависимости от цели производства.

Предположим, что цель рассматриваемого предприятия заключается в получении максимального дохода

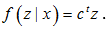
Тогда функцию, равную максимальному доходу для набора товаров x

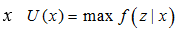
будем называть функцией полезности производственного потребления.

Очевидно, что U(x)=c^tz_*. Если рассматривать Т-двойственную задачу производственного потребления (4), то согласно приведенной выше первой теореме двойственности U(x)=minФ=x^ty_*^’.

Максимизация полезности считается основным мотивом производственного потребительского поведения в экономике. Также в экономической теории важную роль играют предельные полезности, которые показывают численное значение дополнительной полезности, полученной предприятием от использования дополнительной единицы ресурса x [7].

Рассматривая U(x) как полезность выбранного набора ресурсов x, получим, что предельная полезность MU_i(x) i-го ресурса определяется как частная производная функции полезности U(x) по количеству потребляемого блага x_i. В силу третьей теоремы двойственности получается, что вектор предельных полезностей пропорционален вектору оптимальных теневых цен MU(x)=y_*^’.

С понятием функции полезности неразрывно связано и понятие предельной нормы замещения. Из второй теоремы двойственности известно, что теневые цены есть показатель дефицитности ресурсов x. В результате возникает естественный вопрос: можно ли один ресурс заменить на какой-либо другой при неизменном уровне полезности?

Пусть потребление всех товаров, за исключением i-го и j-го, постоянно. Тогда величину

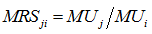
называют предельной нормой замещения i-го товара j-м. MRS определяет количество i-го товара, от которого необходимо отказаться для приобретения дополнительной единицы j-го товара, оставаясь при этом с тем же уровнем полезности.

Как уже было сказано, в случае оптимального решения предприятие находится в точке равновесия потребителя, когда желания предприятия совпадают с его возможностями. В такой ситуации выполняется соотношение

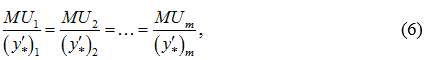
называемое условием равновесия предприятия. Здесь MU_i — предельная полезность используемого i-го ресурса, (y_*^’)_i — его «внутренняя» цена.

Хотелось бы отметить, что в силу равенства y_*= y_*^’, предельные полезности, предельные нормы замещения и условие равновесия предприятия (6) не зависят от выбранного конуса.

Выводы. Исследование задачи линейного программирования с ограничениями конусного типа и двойственных к ней задач показало справедливость следующих моментов. При переносе производственной задачи линейного программирования с конусными ограничениями в пространство новых переменных возникает некоторая другая задача линейного программирования, которая описывает несуществующее, фиктивное предприятие. Показано, что у исходного и фиктивного предприятий совпадают не только «внутренние» теневые цены на факторы производства, но и значения таких экономических характеристик, как предельные нормы замещения и предельные полезности. Условия равновесия этих двух предприятий также тождественны друг другу.

Список использованных источников

1. Кочегурова, Е. А. Теория и методы оптимизации: учебное пособие для академического бакалавриата / Е. А. Кочегурова. — Москва: Издательство Юрайт, 2018. — 133 с.
2. Севодин, М.А., Старкова, Е.О. О производственной задаче с ограничениями конусного типа // Московский экономический журнал, 2018 №5 (3) – С. 378-388.
3. Черников, Ю.Г. Системный анализ и исследование операций: Учебное пособие для вузов / Ю.Г. Черников — М: Издательство Московского государственного горного университета, 2006. – 370 с.
4. Виноградова, Г.В. Моделирование производственно-инвестиционной деятельности фирмы: Учеб. Пособие для вузов / под ред. Виноградова Г.В. – М.: ЭНИТИ-ДАНА, 2002. – 319 с.
5. Лопатников, Л.И. Экономико-математический словарь: Словарь современной экономической науки. – 5-е изд, перераб. и доп. – М.: Дело, 2003. – 520 с.
6. Кремер, Н.Ш., Путко, Б.А., Тришин, И.М., Фридман, М.Н. Исследование операций в экономике: учеб. пособие для вузов / Н. Ш. Кремер, Б. А. Путко, И. М. Тришин, М. Н. Фридман; под ред. Н. Ш. Кремера. — 3-е изд., перераб. и доп. — М. : Издательство Юрайт ; ИД Юрайт, 2013. — 438 с.
7. Альсевич, В.В. Введение в математическую экономику. Конструктивная теория: Учебное пособие. – М.: Едиториал УРСС, 2005. – 256 с.