УДК 519.852

Старкова Екатерина Олеговна, бакалавр, Пермский национальный исследовательский политехнический университет

Научный руководитель: Севодин Михаил Алексеевич, к.ф.-м.н., доцент, Пермский национальный исследовательский политехнический университет

О ЗАДАЧЕ КРЕДИТНОЙ ПОЛИТИКИ БАНКА С ОГРАНИЧЕНИЯМИ КОНУСНОГО ТИПА

ABOUT THE TASK OF THE CREDIT POLICY OF THE BANK WITH CONE TYPE RESTRICTIONS

Аннотация. В данной статье рассматривается задача кредитной политики банка, которая имеет естественные ограничения конусного типа. Показывается, что можно упростить нахождение оптимального решения задачи путем ее перехода из исходной прямоугольной системы координат в многогранный выпуклый конус, находящийся в положительном октанте. Для этого строится новый базис, который представляет собой систему векторов, выпуклая оболочка которых является многогранным конусом.

Summary. This article discusses the task of a bank’s credit policy, which has natural limitations of the conical type. It is shown that it is possible to simplify the search for the optimal solution of the problem by moving it from the original rectangular coordinate system to the multi-faceted convex cone located in the positive octant. For this purpose, a new basis is built, which is a system of vectors whose convex hull is a multi-faceted cone.

Ключевые слова: конус, базис, ограничения конусного типа, линейное программирование.

Keywords: cone, basis, cone constraints, linear programming.

   Введение. В экономике довольно часто приходится иметь дело с экстремальными задачами, для решения которых применяются методы линейного программирования. Один из самых широко применимых методов является симплекс-метод, основанный на целенаправленном переборе вершин выпуклого многогранника [1]. Но, не смотря на его эффективный алгоритм, было показано, что требуемое машинное время на решение задачи линейного программирования с m ограничениями пропорционально , а среднее число итераций равно 2m [2]. Число ограничений задачи оказывает большое влияние на вычислительную эффективность данного метода. Поэтому для уменьшения числа итераций и затрат машинного времени был рассмотрен новый алгоритм нахождения оптимального решения задачи линейного программирования специального вида, который заключается в редуцировании задачи в пространство новых переменных. Для этого среди ограничений задачи выделяется неравенства, задающие многогранный выпуклый конус. После чего по конусным ограничениям строится матрица перехода из старого базиса в новый и совершается переход в новую аффинную систему координат. В конечном итоге получается новая задача в новых переменных, оптимальный план которой можно найти симплекс-методом. Затем совершается обратный переход к старому базису.

   Разберем алгоритм на примере задачи кредитной политики банка [3].

   Пример. Рассмотрим банк, предоставляющий полный набор банковских услуг и находящийся в процессе формирования портфеля кредитов объемом 12 миллионов долларов. В табл.1 представлены возможные типы банковских кредитов.

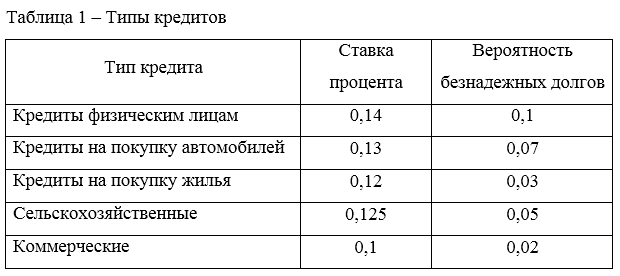
   Безнадежные долги считаются невозвратимыми, поэтому они должны вычитаться из возможного дохода.

   Конкурентная борьба с другими финансовыми институтами вынуждает банк не менее 40% капитала помещать в сельскохозяйственные и коммерческие кредиты. Для содействия строительной индустрии своего региона банк планирует вложить в кредиты на покупку жилья не менее 50% от общей суммы кредитов физических лиц, на покупку автомобилей и жилья. Банк также поддерживает государственную политику, указывающую, что отношение безнадежных долгов ко всей сумме кредитов не должно превышать 0,04.

   Банк желает максимизировать чистую прибыль, т.е. разность между доходом от инвестируемых сумм и суммой невозвращенных кредитов. Так как безнадежные долги считаются невозвратимыми, они вычитаются как из инвестируемых сумм, так и общей прибыли.

   Причем предполагается, что все кредиты выделяются примерно в одно и то же время, что позволит игнорировать временной фактор в процессе размещения капитала в различные кредиты.

   Построим математическую модель данной задачи.

   Положим

 — кредиты физическим лицам;

 — кредиты на покупку автомобилей;

 — кредиты на покупку жилья;

 — сельскохозяйственные кредиты;

 — коммерческие кредиты.

   Задача имеет следующие ограничения.

1. Общая сумма кредитов не должна превышать 12 млн. долларов:

2. Ограничение на сельскохозяйственные и коммерческие кредиты: 

3. Ограничения кредитов на покупку жилья:

4. Ограничения на невозвращенные кредиты:

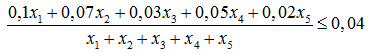
или

   Максимизировать: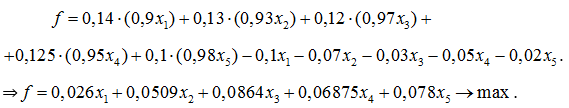 

   Таким образом, получаем следующую задачу линейного программирования:

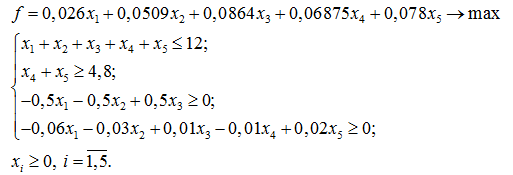
   Среди ограничений выделим группу неравенств, каждое из которых имеет конусный тип:

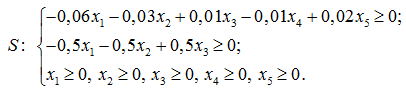
   По данной системе из   неравенств составим матрицу ограничений:

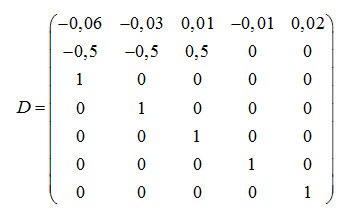
   Для перехода из старой системы координат в новую систему координат построим новый базис – систему векторов, которые образуют многогранный выпуклый конус, находящийся в положительном октанте [4]. Для этого возьмем некоторый  — мерный положительный вектор-строку  и построим уравнение . Затем с учетом найденного уравнения находим крайние точки выпуклого многогранника, построенного по неравенствам системы . После чего по найденным точкам строим новый базис.

   Возьмем в качестве  вектор с координатами равными единице. Тогда ввиду вышесказанного получим следующее уравнение:

   Обозначим символом  систему, полученную в результате замены в  всех знаков неравенства равенствами. В эту же систему добавим найденное выше уравнение.

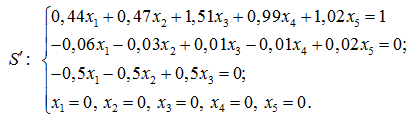
   Найдем все крайние точки полученной системы , причем точки должны удовлетворять системе ограничений . Для этого воспользуемся алгоритмом поиска крайних точек, описанным в [5].

   Получились следующие крайние точки: 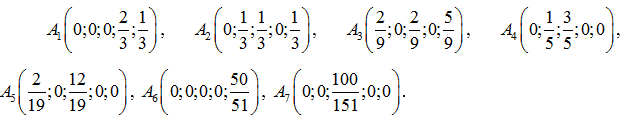. Тогда можно построить базисные вектора  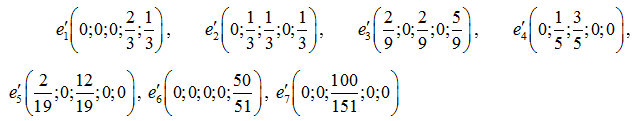и матрицу перехода:

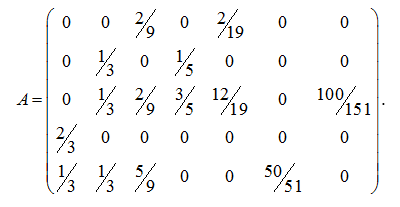
   В данной задаче получилось, что количество образующих многогранного конуса больше, чем размерность исходной задачи.

   Выражаем старые координаты точки  через новые  по формуле:  [6].

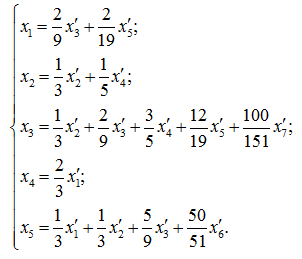
   В результате получаем задачу в новых координатах с семью переменными, но уже с меньшим количеством основных ограничений, что существенно упрощает поиск оптимального решения:

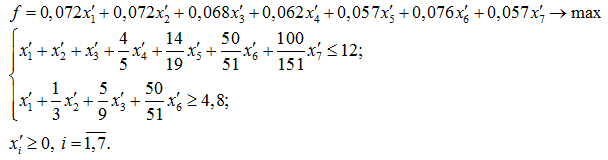
   Находим решение сформулированной задачи симплекс-методом и возвращаемся к старым  координатам.

   В конечном счете, получаем следующий оптимальный план исходной задачи, при котором целевая функция будет равна :

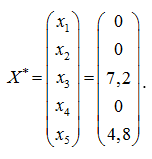
   Резюмируя вышеизложенное, можно сделать вывод, что для получения максимального чистого дохода в размере 0,9965 миллиона долларов банку следует использовать только кредиты на покупку жилья и коммерческие кредиты.

Литература

1. Кормен Т.Х., Лейзерсон Ч.И., Ривест Р.Л., Штайн К. Алгоритмы: построение и анализ, 2-е издание: Пер. с англ. – М.: Издательский дом «Вильямс», 2005. – 1296 с. : ил.
2. Кульневич А. Д. Линейное программирование // Молодой ученый. — 2017. — №10. — С. 29-32. – URL: https://moluch.ru/archive/144/40399/ (дата обращения 27.12.2018).
3. Таха Х.А. Введение в исследование операций. – М.: Издательский дом «Вильямс», 2005. – 912 с.
4. Никайдо Х. Выпуклые структуры и математическая экономика. М: Мир., 1972. – 519 с.
5. Тищенко А.В. Линейная алгебра. Элементы аналитической геометрии. – М.: Финакадемия, 2009. – 116 с.
6. Александров П.С. Лекции по аналитической геометрии. М.: Наука., 1968. — 912 с.